Research

Here are some of the projects I haven been working on throughout my undergraduate study. Topics include theoretical cosmology, astrophysics, mathematics, and computational chemistry.

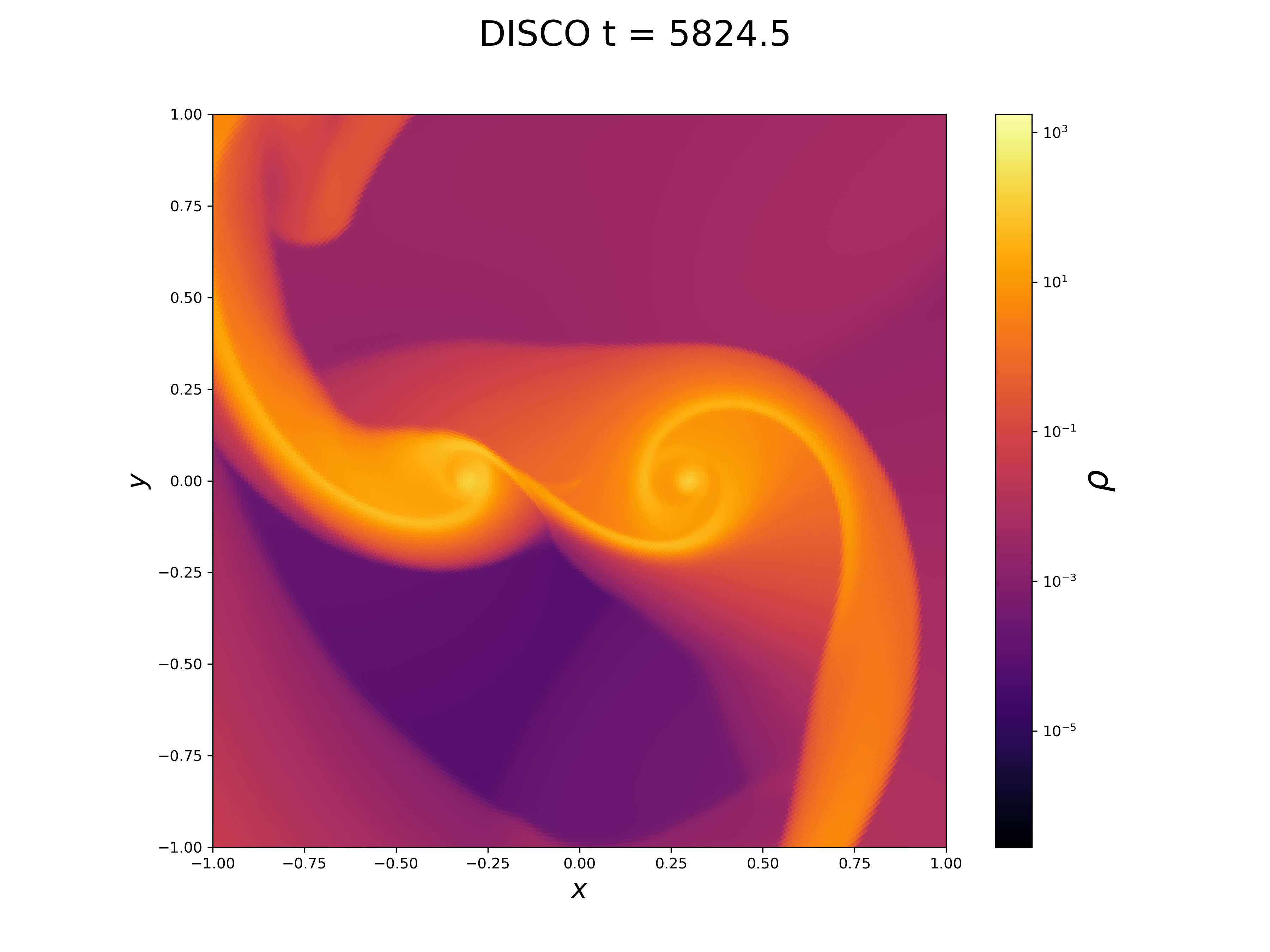
Plasma Dynamics Around Eccentric Binary Black Holes

I explored how eccentric orbits affect gas around binary black holes (BBHs). We performed Python analysis on simulations run by DISCO hydrodynamics code for astrophysical disks mainly to answer these two questions: 1.Does a stable eccentricity point exist? 2.How to determine the radius of a minidisk and would its total mass reach a certain stable value?

Supervised by: Geoffrey Ryan, Ph.D.; Luciano Combi, Ph.D.(Perimeter Institute for Theoretical Physics)

MIT Summer Research Program (MSRP)

GitHub repo can be found here.

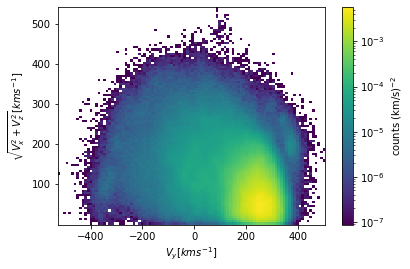
Using Machine Learning to Catalog Accreted Stars in Gaia ESA DR3 Survey

I am following the machine learning framework elaborated in this paper to develop an algorithm to determine which stars are accreted (merged with) into the Milky Way and which are in situ (born within).

Supervised by: Lina Necib, Ph.D. (MIT Kavli Institute for Astrophysics and Space Research)

MIT Summer Research Program (MSRP)

Project ongoing.

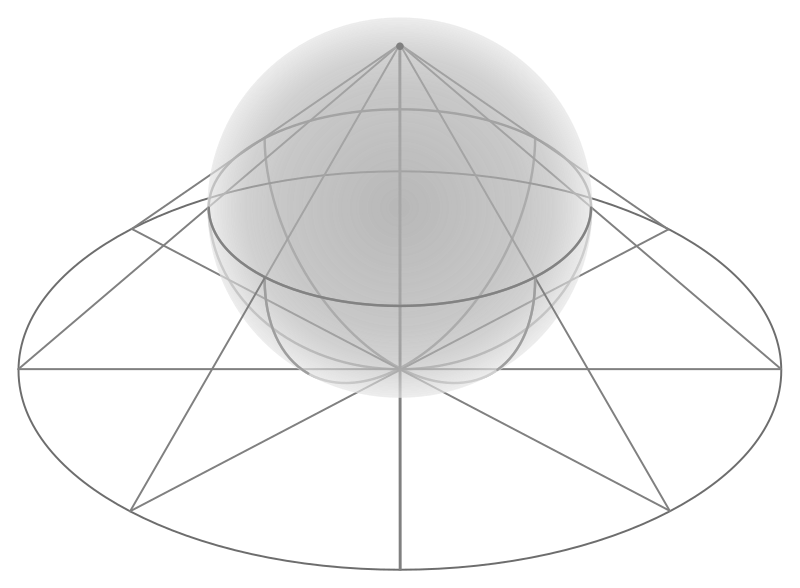
Dark Energy and Dark Matter as Five-Dimensional Stereographic Projection

The purpose of this research is to investigate the nature of dark matter and dark energy using higher- dimensional analysis. The de Sitter metric, describing an empty universe with a positive cosmological constant, can be represented as the four-dimensional hypersurface of a five-dimensional hypersphere of constant curvature. Using the stereographic coordinates, that hypersurface can be projected onto a four-dimensional hyperplane with a conformally flat metric. Dark energy may therefore be a manifestation of constant curvature in the fifth dimension. We repeat these calculations for a universe with a single supermassive black hole in the presence of the cosmological constant, described by the Kottler (Schwarzschild-de Sitter) metric. We aim to determine the corrections from the black hole to the conformally flat metric on the stereographic hyperplane. They could have a form of a polynomial involving the cosmological constant. We aim to investigate if such corrections could mimic dark matter.

Supervised by: Nikodem Poplawski, Ph.D., Kevin Green, Ph.D. (Department of Mathematics and Physics, University of New Haven)

Summer Undergraduate Research Fellowship (SURF), McHale Fellow

Report can be found here.

Computational Analysis on Nucleation Mechanisms of Atmospheric Nitrate and Ammonia Clusters.

As the lead in the computation of the project, I wrote bash scripts and ran optimization jobs on ABCluster and Gaussian. The initial geometries are constructed using Avogadro software. Clusters are formed and optimized by ABCluster, and subsequently Gaussian16 is used to further optimize the selected geometries and deliver the lowest energy geometry. I started with up to 1000 structures and each step reduces the number of geometries by a factor of 10.

Supervised by: Chong Qiu, Ph.D., Dequan Xiao, Ph.D. (Chemical Engineering Department, University of New Haven)

Project ongoing.

Tangent Function as a Solution of a 3-Dimensional Functional Equation

Taking a cue from the identity for the tangent of the sum of three angles, we form a corresponding functional equation in three variables. Then, supposing the function to be differentiable, we solve the functional equation and conclude that the solution is essentially the tangent function up to a constant multiple of the argument variable. The methodology used can be understood by a student with a background in multivariable calculus.

Supervised by: Ramesh Sharma, Ph.D. (Department of Mathematics and Physics, University of New Haven)

Submitted paper can be found here.